Формулы и справочные материалы для успешной подготовки к ЕГЭ по математике

Подготовка к экзамену ЕГЭ по математике требует систематического изучения различных тем, методик и примеров задач. Надёжные справочные материалы помогут не только углубить знания, но и освоить методы решения разнообразных задач, что важно для успешного прохождения экзамена.

Базовый уровень

ЕГЭ по математике базового уровня — это экзамен по математике для выпускников школ, которые выбирают базовый уровень сложности этого предмета для сдачи. Этот уровень предусматривает базовый курс математики, который охватывает основные темы, методы и применения в рамках школьной программы.

На экзамене ЕГЭ по математике базового уровня задания ориентированы на проверку базовых знаний и умений, не требуя глубокого понимания более сложных математических концепций. Он предоставляет возможность выпускникам показать свои базовые математические знания и навыки в решении стандартных задач.

Результаты сдачи ЕГЭ по базовому уровню математики могут использоваться для поступления в учебные заведения, где не требуется продвинутый уровень знаний по математике, или в случае, если абитуриент выбирает специальности, не связанные с глубоким изучением этого предмета.

Алгебра

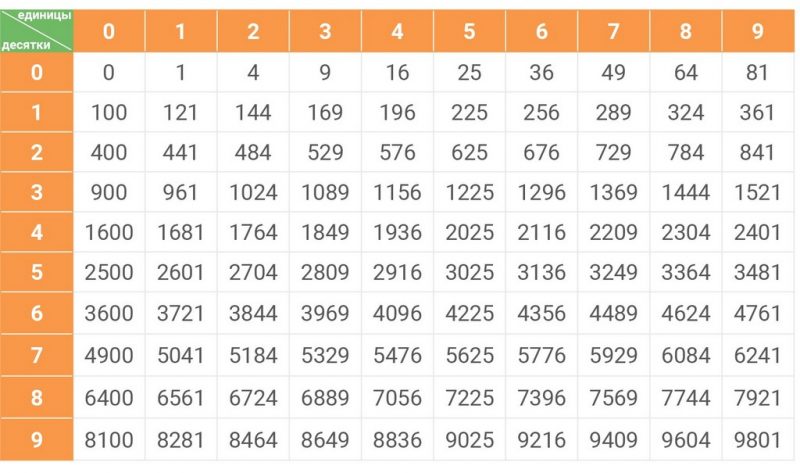
Таблица квадратов целых чисел от 0 до 99

Таблица квадратов целых чисел от 0 до 99 представляет собой набор результатов возведения каждого числа от 0 до 99 в квадрат. Эта таблица часто используется в математике и других областях для быстрого определения квадратов чисел и выполнения различных вычислений. В ней представлены значения их квадратов, что облегчает работу с числами и упрощает процесс вычислений и анализа данных.

Свойства арифметического квадратного корня

Арифметический квадратный корень является одной из важных математических операций, обратной операции возведения числа в квадрат. Он обозначается символом √ и позволяет найти такое число, которое возводя его в квадрат, даст исходное число.

Некоторые из основных свойств арифметического квадратного корня:

1. √a * √b = √(a * b): Это свойство позволяет перемножать квадратные корни отдельных чисел и получать квадратный корень от их произведения.
2. √(a / b) = √a / √b: Оно предоставляет возможность разделять квадратные корни чисел, находя корень от частного, как отношение корней отдельных чисел.
3. √(a^2) = |a|: Корень из квадрата числа равен модулю этого числа, так как возврат из квадрата убирает отрицательность.
4. √(a^n) = |a^(n/2)|: Квадратный корень из степени числа равен модулю этого числа, возведенного в степень, деленной на 2.

Эти свойства помогают упростить вычисления и проведение операций с квадратными корнями в математических задачах.

Корни квадратного уравнения

Квадратное уравнение — это уравнение второй степени, представляемое обычно в виде ax2+bx+c=0ax2+bx+c=0, где $a$, $b$ и $c$ — коэффициенты, причем a≠0a=0.

Решения квадратного уравнения находятся с помощью формулы квадратного корня:

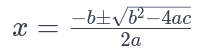
Где D = b²−4ac называется дискриминантом. Он определяет тип корней:

1. Если $D>0$, уравнение имеет два различных действительных корня.
2. Если $D=0$, уравнение имеет один действительный корень (корень кратности два).
3. Если $D<0$, уравнение имеет два комплексных корня.

Эти корни могут быть найдены, используя формулу квадратного корня.

Формулы сокращённого умножения

Сокращённое умножение в математике — это способ умножения чисел, используя свойства арифметики для упрощения выражений. Некоторые формулы сокращённого умножения:

1. Квадрат суммы двух чисел: (a+b)²=a²+2ab+b²
2. Квадрат разности двух чисел: (a−b)²=a²−2ab+b²
3. Разность квадратов: (a+b)(a−b)=a²−b²
4. Куб суммы двух чисел: (a+b)³=a³+3a²b+3ab²+b³
5. Куб разности двух чисел: (a−b)³=a³−3a³b+3ab²−b³
6. Сумма кубов: a³+b³=(a+b)(a²−ab+b²)

Эти формулы полезны для упрощения выражений, факторизации и вычислений. Их использование помогает оперативно преобразовывать сложные выражения, экономя время и упрощая решение задач.

Степень

Свойства степени в математике представляют основные правила и характеристики работы со степенями чисел.

Эти свойства используются для упрощения выражений, решения уравнений и задач, связанных со степенями и их операциями.

Логарифм

Логарифмы являются мощным инструментом математики, позволяющим работать с большими числами и сложными выражениями. Они связаны с понятием степени и представляют обратную операцию возведения числа в определенную степень. Свойства логарифмов позволяют упрощать сложные выражения, сокращать операции и решать различные математические задачи.

Эти свойства помогают упростить операции, связанные с логарифмами, преобразовать и решать сложные математические задачи.

Геометрия

Стереометрия

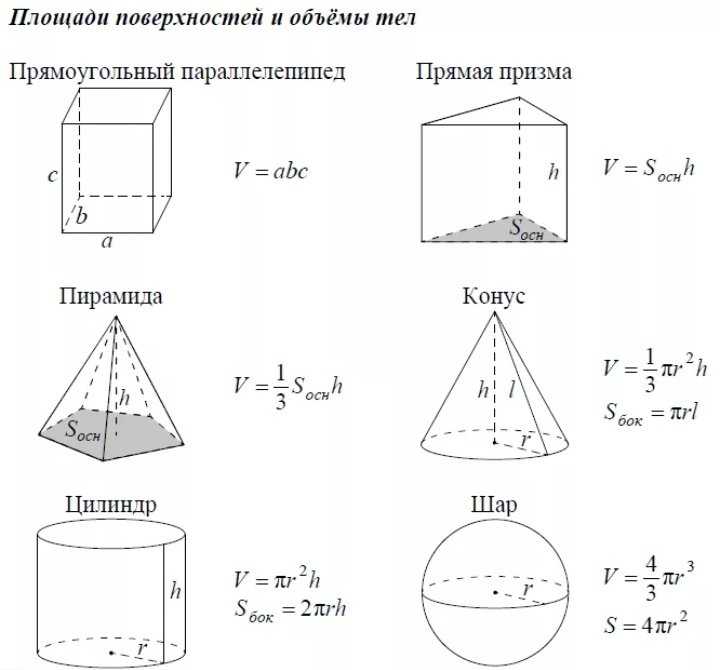
Стереометрия — это раздел геометрии, изучающий фигуры и объекты в трехмерном пространстве. В этом разделе математики важными являются формулы, которые позволяют определять объемы, площади поверхностей, длины ребер и другие параметры трехмерных фигур. Формулы стереометрии применяются в различных областях, включая архитектуру, инженерное дело, физику и другие науки.

Они позволяют рассчитывать объемы таких фигур, как параллелепипеды, призмы, пирамиды, конусы, цилиндры и многогранные тела. Формулы стереометрии также помогают определять расстояния между точками в трехмерном пространстве, а также находить площади поверхностей фигур.

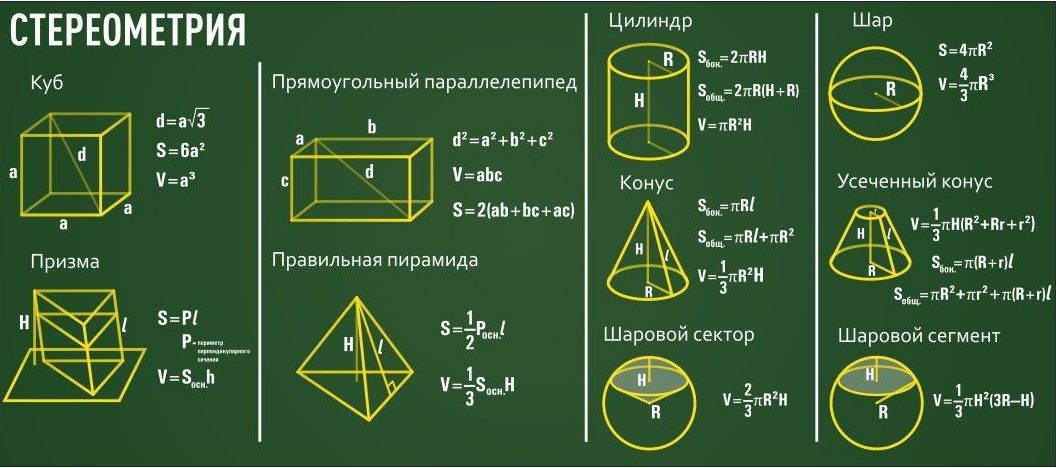
Изучение этих формул позволяет не только эффективно решать задачи в трехмерной геометрии, но и применять их для практических задач, связанных с построением, дизайном, инженерией и другими областями, где важно учитывать трехмерные параметры объектов и фигур.

Справочные материалы по математике представляют собой надёжный инструмент для подготовки к экзамену ЕГЭ. Приобретение уверенности в решении разнообразных задач и овладение ключевыми методами помогут абитуриентам успешно справиться с экзаменом, достичь высоких результатов и реализовать свой потенциал в этом предмете.

Рекомендуем по теме

Словарь литературных терминов для ЕГЭ

Основные даты в истории России для сдачи ЕГЭ

План сочинения ЕГЭ по русскому языку 2023

План анализа стихотворения по литературе

Равнобедренный треугольник: определение и свойства

Формула и определение первого закона Ньютона