Равнобедренный треугольник: определение и свойства
Равнобедренный треугольник — это треугольник, у которого две стороны равны между собой. Такие стороны называются боковыми сторонами, а третья сторона называется основанием.
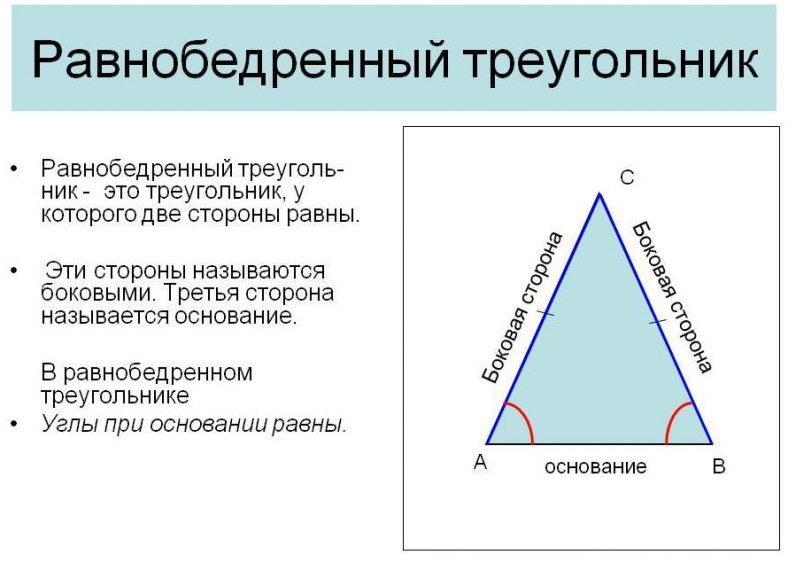
АС = СB — боковые стороны
АB — основание
Содержание
Свойства равнобедренного треугольника
Равнобедренные треугольники обладают пятью основными теоремами, которые описывают их свойства.
Теорема 1
В равнобедренном треугольнике углы при основании равны.
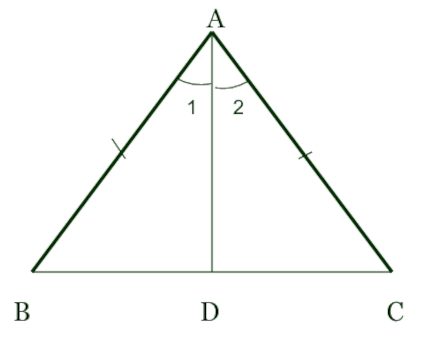
Доказательство. Пусть у нас есть равнобедренный треугольник ABC, в котором AB = AC. Нам нужно показать, что углы при основании, то есть угол B и угол C, равны между собой.
Рассмотрим треугольник ABC. У нас уже известно, что AB = AC. Рассмотрим два случая:
- Пусть угол ABC равен углу ACB: В этом случае у нас имеется две равные стороны AB и AC, а также угол ABC равен углу ACB по построению. Согласно теореме о равенстве углов при основании равнобедренного треугольника, угол B равен углу C.
- Пусть угол ABC не равен углу ACB: В этом случае у нас имеется две равные стороны AB и AC, но угол ABC не равен углу ACB. Предположим, что угол B больше угла C. Тогда, по теореме о треугольнике, сумма углов в треугольнике ABC равна 180 градусов. Мы можем записать это следующим образом: угол A + угол B + угол C = 180 градусов угол A + угол C + угол C = 180 градусов (угол A + 2 * угол C) = 180 градусов угол A + 2 * угол C > 180 градусов (так как угол B больше угла C) Это противоречит аксиоме, согласно которой сумма углов в треугольнике равна 180 градусов. Следовательно, предположение неверно, и угол B не может быть больше угла C.
Таким образом, мы показали, что в равнобедренном треугольнике углы при основании, угол B и угол C, равны между собой.
Теорема 2
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Доказательство. Пусть у нас есть равнобедренный треугольник ABC, в котором AB = AC. Мы хотим показать, что биссектриса BD, проведенная к основанию BC, является медианой и высотой треугольника.
- Докажем, что BD является медианой: Рассмотрим треугольник ABD. У нас уже известно, что AB = AD, так как треугольник равнобедренный. Также мы знаем, что угол B равен углу D, так как это равнобедренный треугольник. Из этих двух равенств следует, что треугольник ABD — равнобедренный треугольник. Медиана в треугольнике делит противоположную сторону пополам. Так как AB = AD, биссектриса BD делит сторону AC пополам. Следовательно, биссектриса BD является медианой треугольника ABC.
- Докажем, что BD является высотой: Рассмотрим треугольник BCD. У нас уже известно, что AB = AC, поэтому углы B и C равны между собой. Рассмотрим угол BCD. Поскольку треугольник равнобедренный, угол B равен углу C. Значит, угол BCD является прямым углом. В равнобедренном треугольнике высота проведена из вершины к основанию, перпендикулярно к основанию. Следовательно, BD, проведенная из вершины B, является высотой треугольника ABC.
Таким образом, мы показали, что биссектриса BD, проведенная к основанию BC, одновременно является медианой и высотой равнобедренного треугольника ABC.
Теорема 3
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Доказательство. Пусть у нас есть равнобедренный треугольник ABC, в котором AB = AC. Мы хотим показать, что медиана BD, проведенная к основанию BC, является биссектрисой и высотой треугольника.
- Докажем, что BD является биссектрисой: Рассмотрим треугольник ABD. У нас уже известно, что AB = AD, так как треугольник равнобедренный. Также мы знаем, что угол B равен углу D, так как это равнобедренный треугольник. Из этих двух равенств следует, что треугольник ABD — равнобедренный треугольник. Биссектриса в треугольнике делит противоположный угол пополам. Так как угол B равен углу D, биссектриса BD делит угол A пополам. Следовательно, биссектриса BD является биссектрисой треугольника ABC.
- Докажем, что BD является высотой: Рассмотрим треугольник BCD. У нас уже известно, что AB = AC, поэтому углы B и C равны между собой. Рассмотрим угол BCD. Поскольку треугольник равнобедренный, угол B равен углу C. Значит, угол BCD является прямым углом. В равнобедренном треугольнике высота проведена из вершины к основанию, перпендикулярно к основанию. Следовательно, BD, проведенная из вершины B, является высотой треугольника ABC.
Таким образом, мы показали, что медиана BD, проведенная к основанию BC, одновременно является биссектрисой и высотой равнобедренного треугольника ABC.
Теорема 4
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство. Пусть у нас есть равнобедренный треугольник ABC, в котором AB = AC. Мы хотим показать, что высота, проведенная к основанию BC, является одновременно биссектрисой и медианой треугольника.
- Докажем, что высота BD является биссектрисой: Рассмотрим треугольник ABD. У нас уже известно, что AB = AD, так как треугольник равнобедренный. Пусть высота BD пересекает сторону AC в точке E. Мы хотим показать, что угол ABE равен углу DBE. Так как BD является высотой, угол DBE будет прямым. Также, так как треугольник ABD равнобедренный, угол ABD равен углу ADB. Так как угол ABD равен углу ABE (поскольку BE является продолжением BD), то получаем, что угол ABE равен углу ADB. Таким образом, высота BD является биссектрисой треугольника ABC.
- Докажем, что высота BD является медианой: Рассмотрим треугольник BDC. У нас уже известно, что AB = AC, поэтому углы B и C равны между собой. Пусть высота BD пересекает сторону BC в точке F. Мы хотим показать, что BF = FC. Так как BD является высотой, угол BDF будет прямым. Также, так как треугольник BDC равнобедренный, угол BCD равен углу BDC. Так как угол BCD равен углу BDF (поскольку DF является продолжением BD), то получаем, что угол BDF равен углу BDC. Из этого следует, что треугольники BDF и BDC подобны. Поскольку треугольники BDF и BDC подобны, то соответствующие стороны пропорциональны. То есть, BF/BD = BC/BD. Сокращая BD, получаем, что BF = BC. Значит, точка F делит сторону BC пополам, что означает, что высота BD является медианой треугольника ABC.
Таким образом, мы показали, что высота, проведенная к основанию BC, в равнобедренном треугольнике одновременно является биссектрисой и медианой треугольника ABC. Это доказывает связь между этими трехсоставляющими треугольника.
Биссектриса делит угол между боковыми сторонами треугольника на две равные части. В нашем случае, высота BD является биссектрисой угла BAC, так как она перпендикулярна стороне BC и делит угол BAC на две равные части. Это дает нам равенство углов DBA и DBC.
Медиана треугольника является отрезком, соединяющим вершину треугольника с серединой противоположной стороны. В нашем случае, высота BD также является медианой треугольника ABC, так как она соединяет вершину A с серединой стороны BC. Так как треугольник ABC равнобедренный, то медиана BD делит сторону BC пополам, что означает, что BF = FC.
Теорема 5
Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство от противного. Предположим, что у нас есть два треугольника, A и B, и известно, что все три стороны треугольника A равны трем сторонам треугольника B. Мы предполагаем, что треугольники A и B не равны.
Поскольку все три стороны треугольника A равны трем сторонам треугольника B, мы можем сделать следующие утверждения:
Сторона AB треугольника A равна стороне BC треугольника B.
Сторона BC треугольника A равна стороне CA треугольника B.
Сторона CA треугольника A равна стороне AB треугольника B.
Теперь предположим, что треугольники A и B не равны. Значит, у них должно быть хотя бы одно отличие.
Пусть, например, угол ∠C треугольника A отличается от угла ∠C треугольника B. Это означает, что угол ∠C треугольника A не равен углу ∠C треугольника B.
Но по условию известно, что стороны треугольника A равны сторонам треугольника B. Значит, треугольники имеют соответственные углы равными, так как соответствующие углы треугольников равны при равенстве соответствующих сторон.
Таким образом, мы пришли к противоречию: углы ∠C треугольника A должны быть равны углу ∠C треугольника B, но предположение о неравенстве треугольников приводит к тому, что углы не равны.
Следовательно, наше предположение о неравенстве треугольников было ошибочным. Треугольники A и B должны быть равны, если все три их стороны равны.
Таким образом, доказательство от противного подтверждает утверждение: если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника равна 180°.
- Если биссектриса треугольника является медианой или высотой.
- Если медиана треугольника является биссектрисой или высотой.
- Если высота треугольника является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника

Формулы длины стороны (основания — b):
- b = 2a sin( β/2 )=a √(2−2cosβ)
Формулы длины равных сторон — (а):
- a = b / 2 sin(/2) = b / √(2−2cos
- a = b / 2cos α
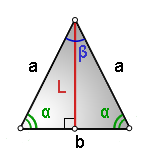
L — высота=биссектриса=медиана
b — сторона (основание)
а — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- = (b/2) * tgα
- = (1+cosβ)/2= cos(β) / 2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
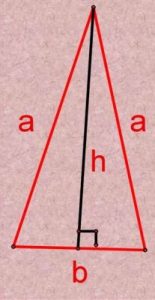
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):

