Как возникла геометрия: история и развитие науки
Геометрия, одна из самых древних математических дисциплин, имеет долгую и увлекательную историю, уходящую корнями в глубокую древность. От своего появления в форме практических знаний у древних цивилизаций до развития в теоретическую науку в античной Греции, геометрия прошла долгий путь. В этом тексте мы рассмотрим основные этапы её развития и проследим, как менялись представления о пространственных отношениях и фигурах на протяжении тысячелетий.
Слово «геометрия» происходит от греческих слов «гео» (земля) и «метрео» (измерять) и буквально переводится как «измерение земли». Это название отражает первоначальные практические цели дисциплины. Первые примитивные формы геометрии возникли из необходимости измерять землю, строить здания, определять границы земельных участков и рассчитывать площади полей.
Содержание
Египет: начало измерений
Древний Египет считается одной из первых цивилизаций, где началась разработка геометрических знаний. Это объясняется необходимостью измерять и восстанавливать границы земельных участков после ежегодных разливов Нила. В результате наводнений границы полей размывались, и египтянам приходилось восстанавливать их. Эти задачи требовали применения знаний о формах и их размерах, что привело к возникновению начальных принципов геометрии.
Среди археологических находок, подтверждающих наличие геометрических знаний у египтян, выделяются «Математический папирус Ринда» и «Московский математический папирус», датируемые приблизительно 1850 годом до н. э. Эти документы содержат задачи на вычисление площадей простых фигур: треугольников, прямоугольников и трапеций. Хотя методы египтян были далеки от современных, они заложили основу будущих геометрических изысканий.
Вавилон: развитие геометрических знаний
Вавилонская цивилизация также внесла значительный вклад в развитие геометрии. В отличие от египтян, вавилоняне записывали свои знания на глиняных табличках клинописью, многие из которых сохранились до наших дней. Эти таблички содержат примеры задач по вычислению площадей прямоугольников и трапеций, а также объёмов простых трёхмерных тел, таких как цилиндры и призмы.
Особенностью вавилонской геометрии является использование шестидесятеричной системы счисления, которая сохранилась в астрономии и измерении времени до наших дней (60 минут в часе, 360 градусов в круге). Вавилоняне применяли геометрию не только для измерений земли, но и для астрономических расчетов, что свидетельствует о широте их математических знаний.
Античная Греция: зарождение теоретической геометрии
Настоящий расцвет геометрии как науки произошел в Древней Греции. Именно здесь геометрия приобрела теоретический характер, превратившись из прикладной дисциплины в абстрактную науку о фигурах и их свойствах.
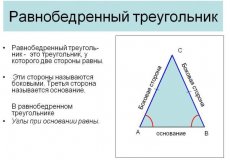
Одним из первых греческих мыслителей, занимавшихся геометрией, был Фалес Милетский (около 624–546 гг. до н. э.). Ему приписывают несколько геометрических открытий, таких как утверждение о том, что диаметр делит круг пополам, и теорему о равенстве углов при основании равнобедренного треугольника. Фалес не просто применял геометрию для практических задач, но и пытался объяснять её логически, что стало первым шагом к теоретической геометрии.
Значительный вклад в развитие геометрии внёс Пифагор Самосский (около 570–495 гг. до н. э.), основавший свою философскую и математическую школу. Ученики Пифагора считали, что весь мир можно объяснить через числа и их соотношения, а геометрия рассматривалась как ключ к пониманию вселенной. Самая известная теорема, связанная с именем Пифагора, — это теорема Пифагора, утверждающая, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора стала важным этапом в развитии геометрии, так как связала алгебраические соотношения с геометрическими фигурами. Школа Пифагора внесла большой вклад в изучение геометрических фигур, их свойств и соотношений, заложив основу для будущих математических открытий.
Наиболее значительным трудом в истории геометрии является «Начала» (лат. «Elementa»), написанный Евклидом около 300 года до н. э. Евклид разработал систему аксиом, из которых выводил все геометрические теоремы логическим путем. Его труд включал 13 книг, в которых рассматривались различные аспекты геометрии: от элементарных понятий точек и линий до сложных трёхмерных тел.
Евклидова геометрия основывалась на пяти аксиомах (или постулатах), из которых самые известные:
- Через любые две точки можно провести прямую линию.
- Любую отрезок можно продолжить в прямую.
- Существуют окружности с любым центром и радиусом.
- Все прямые углы равны между собой.
- Если прямая пересекает две другие, так что сумма внутренних углов меньше двух прямых, то эти две прямые пересекутся при продолжении.
Пятый постулат вызвал множество споров и дискуссий, так как он был сложнее других и не выглядел очевидным. Попытки доказать его привели к развитию новой области математики — неевклидовой геометрии.
Архимед (около 287–212 гг. до н. э.) и Аполлоний Пергский (около 262–190 гг. до н. э.) внесли значительный вклад в развитие геометрии. Архимед изучал кривые и поверхности, такие как параболы, гиперболы и эллипсы. Он разработал методы для вычисления площадей и объёмов сложных фигур, что стало предшественником интегрального исчисления.
Аполлоний Пергский, в свою очередь, посвятил свои исследования коническим сечениям — кругам, параболам, гиперболам и эллипсам. Его труды оказали влияние на развитие астрономии и стали основой для теорий движения планет.
Средневековье и Возрождение: развитие геометрии в разных культурах
После падения Римской империи интерес к геометрии в Европе заметно снизился, однако геометрические знания продолжали развиваться в исламском мире. Арабские учёные переводили труды греческих математиков и развивали геометрию, добавляя свои открытия.
Во время Возрождения европейские учёные снова обратились к геометрии. Одним из значительных шагов стало появление аналитической геометрии, разработанной Рене Декартом в XVII веке. Декарт объединил алгебру и геометрию, введя систему координат, которая позволила описывать геометрические фигуры с помощью уравнений.
Современная геометрия: новые направления
В XIX веке геометрия снова пережила революцию, когда математик Карл Фридрих Гаусс и его последователи, такие как Николай Лобачевский, начали разрабатывать неевклидову геометрию. Лобачевский предположил, что пятый постулат Евклида может быть ложным, и построил геометрию, в которой через точку можно провести множество прямых, не пересекающихся с данной.
Позднее развились такие области, как топология, изучающая свойства фигур, сохраняющиеся при непрерывных деформациях, и дифференциальная геометрия, описывающая кривизну поверхностей. Сегодня геометрия используется в физике, инженерии, компьютерной графике и многих других областях.
История геометрии — это путь от простых практических измерений до абстрактных математических теорий. Она показала, как человеческий разум способен преобразовывать эмпирические знания в строгие научные концепции, и продолжает оставаться важной частью науки и техники.